完全二叉树的定义、性质以及算法见正文。这里补充一点:完全二叉树是效率很高的数据结构,堆是一种完全二叉树或者近似完全二叉树,所以效率极高,像十分常用的排序算法、Dijkstra算法、Prim算法等都要用堆才能优化,几乎每次都要考到的二叉排序树的效率也要借助平衡性来提高,而平衡性基于完全二叉树。
完全二叉树(Complete Binary Tree)
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
一棵二叉树至多只有最下面的一层上的结点的度数可以小于2,并且最下层上的结点都集中在该层最左边的若干位置上,则此二叉树成为完全二叉树。
叶子结点只可能在最大的两层上出现,对任意结点,若其右分支下的子孙最大层次为L,则其左分支下的子孙的最大层次必为L 或 L+1;
出于简便起见,完全二叉树通常采用数组而不是链表存储,其存储结构如下:
var tree:array[1..n]of longint;{n:integer;n>=1}
对于tree[i],有如下特点:
(1)若i为奇数且i>1,那么tree的左兄弟为tree[i-1];
(2)若i为偶数且i<n,那么tree的右兄弟为tree[i+1];
(3)若i>1,tree的父亲节点为tree[i div 2];
(4)若2*i<=n,那么tree的左孩子为tree[2*i];若2*i+1<=n,那么tree的右孩子为tree[2*i+1];
(5)若i>n div 2,那么tree[i]为叶子结点(对应于(3));
(6)若i<(n-1) div 2.那么tree[i]必有两个孩子(对应于(4))。
(7)满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树。
完全二叉树第i层至多有2^(i-1)个节点,共i层的完全二叉树最多有2^i-1个节点。
完全二叉树的特点是:
1)只允许最后一层有空缺结点且空缺在右边,即叶子结点只能在层次最大的两层上出现;
2)对任一结点,如果其右子树的深度为j,则其左子树的深度必为j或j+1。 即度为1的点只有1个或0个
有如下的一颗完全二叉树:
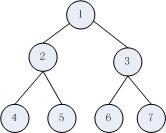
先序遍历结果应该为:1 2 4 5 3 6 7
中序遍历结果应该为:4 2 5 1 6 3 7
后序遍历结果应该为:4 5 2 6 7 3 1
层序遍历结果应该为:1 2 3 4 5 6 7
二叉树的先序遍历、中序遍历、后序遍历其实都是一样的,都是执行递归操作。
我这记录一下层次遍历吧:层次遍历需要用到队列,先入队在出队,每次出队的元素检查是其是否有左右孩子,有则将其加入队列,由于利用队列的先进先出原理,进行层次遍历。
下面记录下完整代码(Java实现),包括几种遍历方法:
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;
/**
* 定义二叉树节点元素
* @author bubble
*
*/
class Node {
public Node leftchild;
public Node rightchild;
public int data;
public Node(int data) {
this.data = data;
}
}
public class TestBinTree {
/**
* 将一个arry数组构建成一个完全二叉树
* @param arr 需要构建的数组
* @return 二叉树的根节点
*/
public Node initBinTree(int[] arr) {
if(arr.length == 1) {
return new Node(arr[0]);
}
List<Node> nodeList = new ArrayList<>();
for(int i = 0; i < arr.length; i++) {
nodeList.add(new Node(arr[i]));
}
int temp = 0;
while(temp <= (arr.length - 2) / 2) { //注意这里,数组的下标是从零开始的
if(2 * temp + 1 < arr.length) {
nodeList.get(temp).leftchild = nodeList.get(2 * temp + 1);
}
if(2 * temp + 2 < arr.length) {
nodeList.get(temp).rightchild = nodeList.get(2 * temp + 2);
}
temp++;
}
return nodeList.get(0);
}
/**
* 层序遍历二叉树,,并分层打印
* @param root 二叉树根节点
*
*/
public void trivalBinTree(Node root) {
Queue<Node> nodeQueue = new ArrayDeque<>();
nodeQueue.add(root);
Node temp = null;
int currentLevel = 1; //记录当前层需要打印的节点的数量
int nextLevel = 0;//记录下一层需要打印的节点的数量
while ((temp = nodeQueue.poll()) != null) {
if (temp.leftchild != null) {
nodeQueue.add(temp.leftchild);
nextLevel++;
}
if (temp.rightchild != null) {
nodeQueue.add(temp.rightchild);
nextLevel++;
}
System.out.print(temp.data + " ");
currentLevel--;
if(currentLevel == 0) {
System.out.println();
currentLevel = nextLevel;
nextLevel = 0;
}
}
}
/**
* 先序遍历
* @param root 二叉树根节点
*/
public void preTrival(Node root) {
if(root == null) {
return;
}
System.out.print(root.data + " ");
preTrival(root.leftchild);
preTrival(root.rightchild);
}
/**
* 中序遍历
* @param root 二叉树根节点
*/
public void midTrival(Node root) {
if(root == null) {
return;
}
midTrival(root.leftchild);
System.out.print(root.data + " ");
midTrival(root.rightchild);
}
/**
* 后序遍历
* @param root 二叉树根节点
*/
public void afterTrival(Node root) {
if(root == null) {
return;
}
afterTrival(root.leftchild);
afterTrival(root.rightchild);
System.out.print(root.data + " ");
}
public stati
.........................................................